Question

Use completing the square to identify the solutions to the quadratic below: d^2 + 4d - 10 = 0

Answer 1

`\begin{gathered} d=-2+\sqrt[]{14} \\ d=-2-\sqrt[]{14} \end{gathered}`

Step-by-step explanation

We want to solve the quadratic equation using completing the square method:

`d^2+4d-10=0`

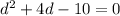
The general form of a quadratic equation is:

`ax^2+bx+c=0`

where a, b and c are coefficients.

The first step is to find a number that is equal to:

`((b)/(2))^2`

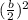
From the given equation, b is 4.

So, we have that:

`((4)/(2))^2=2^2=4`

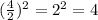
Now, we can add that number to both sides of the equation and write it in this form:

`(d^2+4d+4)-10=4`

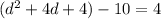
Factorize the part of the left hand side in the parantheses:

`\begin{gathered} (d^2+2d+2d+4)-10=4 \\ (d+2)^2-10=4 \end{gathered}`

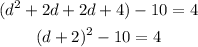
Add 10 to both sides of the equation:

`\begin{gathered} (d+2)^2=4+10 \\ (d+2)^2=14 \end{gathered}`

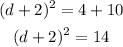
Find the square root of both sides:

`\begin{gathered} d+2=+\sqrt[]{14} \\ \text{and} \\ d+2=-\sqrt[]{14} \end{gathered}`

Subtract 2 from both sides of the equation:

`\begin{gathered} \Rightarrow d=-2+\sqrt[]{14} \\ \text{and} \\ \Rightarrow d=-2-\sqrt[]{14} \end{gathered}`

That is the solution of the equation according to completing the square method.