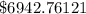Solution:
Given that an investment accout is opend with an initial deposit of $6500, and the account chosen compounds interest annually.
A) Equation to calculate the compunded interest.
The interest is expressed as

B) Value of the account after 10 years, if interest is paid at 3.7%, if no other withdrawals or deposits are made.
This implies that
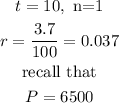
thus,
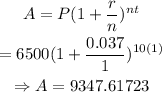
Thus, the value of the account after 10 years is
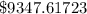
C) Interest earned if the account is left for 20 years.
In this case,
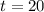
Thus, the interest is evaluated as
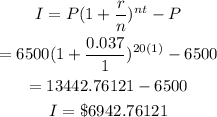
The interest when the account is left alone for 20 years is