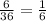Question

A pair of dice are tossed Find the probability that the first roll is a total of at least 5 and the second roll is a total of at least 10

Answer 1

-

Question A:

The pair of dice has a total space f

`6*6=36`

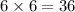
- For the dice to give a total of at least 5, the possible combinations are:

`\begin{gathered} (2,3),(3,2) \\ (2,4),(4,2) \\ (2,5),(5,2) \\ (2,6),(6,2) \\ \\ (3,3) \\ (3,4),(4,3) \\ (3,5),(5,3) \\ (3,6),(6,3) \\ \\ (4,4) \\ (4,5)(5,4) \\ (4,6)(6,4) \\ (4,1)(1,4) \\ (5,5) \\ (5,6)(6,5) \\ (5,1)(1,5) \\ (6,6) \\ (6,1)(1,6) \\ \text{ In total there are 30 possiblilities} \end{gathered}`

- Thus, we have the probability of choosing at least 5 as follows:

`(30)/(36)=(5)/(6)`

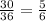
Question B:

- A total of at lest 10 ihas the following possibilities:

`\begin{gathered} (5,5) \\ (4,6),(6,4) \\ \\ (5,6)(6,5) \\ (6,6) \\ \\ \text{ There are 6 possibilities} \end{gathered}`

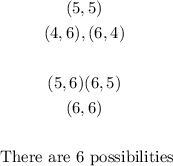
- Thus the probability of the second roll being a total of at least 10 is

`(6)/(36)=(1)/(6)`