Solution:
The provisional equation of the line with slope -4/3 that passes through the point (-4,2) is:
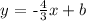
to find b, we can replace in the previous equation, the coordinates of any point of the line and solve for b. For example, we can take the point (x,y)=(-4,2) and we obtain the following equation:
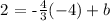
solving for b, we get:
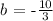
thus, the equation of the line is:

in function notation, this is equivalent to:
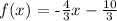
If we graph this function, we obtain the graph of the line:
and, to obtain three points on the line, we can use the formula of the line like this:
for x = 1, then:
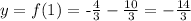
and we obtain the point :

for x = 2, then:

and we obtain the point :

for x = 3, then:
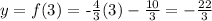
and we obtain the point :
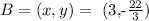
the plot of these three points on the line is: