Question

Solve the multi step problem below Parts a through e (it’s all one question)

Answer 1

Compound Interest

The final value (FV) of an investment P after t years is calculated with the formula:

`FV=P(1+(r)/(m))^(m\cdot t)`

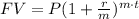
Where r is the annual interest rate and m is the number of compounding periods per year.

We are given the following data:

P = $7000

t = 13 years

r = 7% = 7 / 100 = 0.07

The compounding period varies from part to part.

a) Annually

In this case, m = 1 because the money compounds once per year. Applying the formula:

`FV=7000(1+(0.07)/(1))^(1\cdot13)`

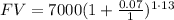
Calculating:

`\begin{gathered} FV=7000(1.07)^(13) \\ \\ FV=16868.92 \end{gathered}`

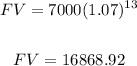
The final value is $16868.92

b) Semiannually. The money compounds twice a year, so m = 2. Applying the formula:

`\begin{gathered} FV=7000(1+(0.07)/(2))^(2\cdot13) \\ \\ FV=7,000(1+0.035)^(26) \\ \\ FV=17121.71 \end{gathered}`

The final value is $17121.71

c) Quarterly. The money compounds 4 times a year, so m = 4. Applying the formula again:

`\begin{gathered} FV=7000(1+(0.07)/(4))^(4\cdot13) \\ \\ FV=7,000(1+0.0175)^(52) \\ \\ FV=17253.92 \end{gathered}`

The final value is $17253.92

d) Daily (calendar year). In this case, we use m = 365:

`\begin{gathered} FV=7000(1+(0.07)/(365))^(365\cdot13) \\ \\ FV=7,000(1+0.0001917808)^(4745) \\ \\ FV=17388.74 \end{gathered}`

The final value is $17388.74

e) Continuously. We use a slightly different formula here:

`FV=P\cdot e^(rt)`

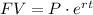
Applying the formula:

`\begin{gathered} FV=7000\cdot e^(0.07\cdot13) \\ \\ FV=17390.26 \end{gathered}`

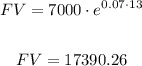
The final value is $17390.26