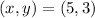The system of equations is given to be:
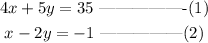
Step 1: Make x the subject of the formula in equation (2)

Step 2: Substitute for x as calculated in equation (3) into equation (1)
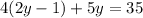
Step 3: Solve the equation from Step 2
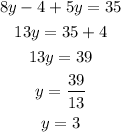
Step 4: Substitute the value of y into equation (3) to get x
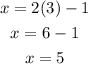
SOLUTION