Question

Given ƒ(x) = 2x² + kx + 19, and the remainder when f(x) is divided by x − 4-is 35, then what is the value of k?

Answer 1

The given function is

`f(x)=2x^2+kx+19`

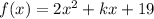
When we divide f by (x - 4) the remainder is 35

That means If we substitute x by 4, the answer should be 35

Then we have to equate x - 4 by 0 first, to get the value of x = 4

Then substitute x by 4 and equate the answer by 35

`\begin{gathered} x-4=0 \\ x-4+4=0+4 \\ x=4 \end{gathered}`
`\begin{gathered} f(4)=35 \\ \\ 2(4)^2+k(4)+19=35 \end{gathered}`

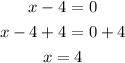
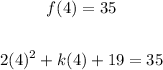
Solve the equation

`\begin{gathered} 2(16)+4k+19=35 \\ \\ 32+4k+19=35 \\ \\ 51+4k=35 \end{gathered}`

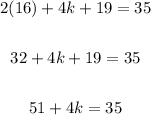
Subtract 51 from both sides

`\begin{gathered} 51-51+4k=35-51 \\ \\ 4k=-16 \end{gathered}`

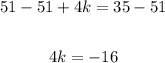
Divide both sides by 4

`\begin{gathered} (4k)/(4)=(-16)/(4) \\ \\ k=-4 \end{gathered}`

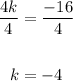
The value of k is -4