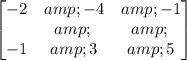d)
Given:
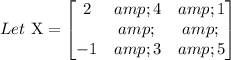
Required:
We need to rotate the triangle by 270 degrees.
Step-by-step explanation:
When rotating a point 270 degrees counterclockwise about the origin our point A(x,y) becomes A'(y, -x). This means, we switch x and y and make x negative.
Switch the first and second row of the given matrix and multiply the first row by (-1).
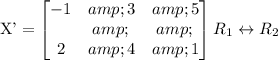
Multiply the first row by (-1).

Answer:
The vertices of the image of the traignle ABC is
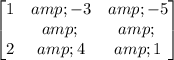
e)
Given:
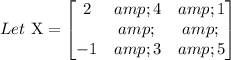
Required:
We need to reflect the triangle across the y-axis.
Step-by-step explanation:
When we reflect a point across the y-axis our point A(x,y) becomes A'(x,-y).
This means making a negative of x.
Multiply the first row by (-1).
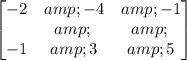
Answer:
The vertices of the image of the traignle ABC is