Given data:
* The initial angular velocity of the turntable is,

* The final angular velocity of the turntable is,
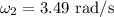
* The mass of the turntable is m = 0.25 kg.
* The diameter of the turntable is D = 30.5 cm.
* The number of revolutions is n = 2.6.
Solution:
The radius of the turntable is,
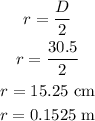
The moment of inertia of turntable is,
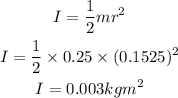
The angular displacement of the turntable is,

By the kinematics equation, the angular acceleration of the turntable in terms of angular velocity and angular displacement is,

Substituting the known values,
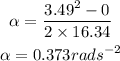
Thus, the torque acting on the turntable is,

Thus, the torque acting on the turntable is,
