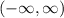Question

Solve the inequality and write final solution in interval notation

Answer 1

Given the following inequality:

`2\lbrack5x-(3x-4)\rbrack>2(2x+3)`

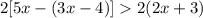
You can solve it as follows:

1. You need to distribute the negative sign on the left side of the inequality:

`2\lbrack5x-3x+4\rbrack>2(2x+3)`

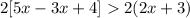
2. You can apply the Distributive Property on both sides of the inequality:

`\begin{gathered} (2)(5x)+(2)(-3x)+(2)(4)>(2)(2x)+(2)(3) \\ 10x-6x+8>4x+6 \end{gathered}`

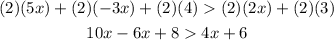
3. Now you can subtract this term from both sides of the inequality:

`\begin{gathered} 10x-6x+8-(4x)>4x+6-(4x) \\ 10x-10x+8>6 \end{gathered}`

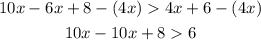
4. You can determine that:

`8>6\text{ (True)}`

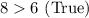
Therefore, you can conclude that all the values of "x" are solutions.

The answer is:

`(-\infty,\infty)`