The sequence for first 41 positive odd numbers is as,
1, 3, 5, 7, 9, ....
This is a arithmetic sequence with first term as a = 1, common difference of d = 2 and number of terms with n = 41.
The formula for the sum of terms in arithmetic sequence is,
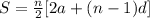
Substitute the values in the formula to determine the sum of first 41 positive odd numbers.
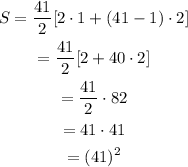
So sum of first 41 positive odd numbers is equal to square of 41. Thus a conjecture can be made that,
The sum is equal to the number of terms squared.