1 Answer

Shulito · Answer 1 · 2023-02-18T17:18:56+0000

Given:

The farmer has 500 yards of fencing with which to enclose a rectangular paddock.

Let x be the width of the rectangle and l be the length of the rectangle.

The equation for the total fencing available is given by,

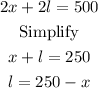
$\begin{gathered} 2x+2l=500 \\ \text{Simplify} \\ x+l=250 \\ l=250-x \end{gathered}$

So, the area is given as,

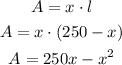
$\begin{gathered} A=x\cdot l \\ A=x\cdot(250-x) \\ A=250x-x^2 \end{gathered}$

Find the critical values,

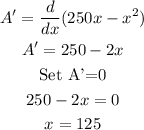
$\begin{gathered} A^(\prime)=(d)/(dx)(250x-x^2) \\ A^(\prime)=250-2x \\ \text{Set A'=0} \\ 250-2x=0 \\ x=125 \end{gathered}$

Test critical value,

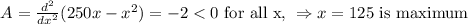
$A^(\doubleprime)=(d^2)/(dx^2)(250x-x^2)=-2<0\text{ for all x, }\Rightarrow x=125\text{ is maximum}$

So, the maximum area is,

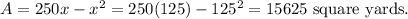
$A=250x-x^2=250(125)-125^2=15625\text{ square yards.}$

Answer: the maximum area is 15625 square yards.

Please log in or register to add a comment.