Answer:
11573.3 cubic feet
Explanations:
The given tent is made up of a rectangular pyramid and prism. The formula for calculating the volume of the tent is expressed as:
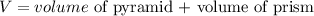
Find the volume of the prism
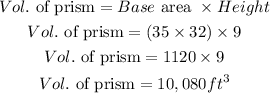
Find the volume of the topped pyramid

Determine the area of the tent
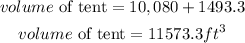
Therefore the total volume of the tent to the nearest tenth is 11573.3 cubic feet