Question

There are 15 boys and 10 girls, out of whom a committee of 3 boys and 2 girls is to be formed. Find the number of ways in which this can be done if i) there is no restriction ii) a particular boy is included iii) a particular girl is excluded

Answer 1

The question provides that there are 15 boys and 10 girls from which a committee of 3 boys and 2 girls is to be formed.

QUESTION I

The number of ways the committee can be chosen when there is no restriction can be calculated as follows:

Number of ways to pick 3 boys from 15:

`15C3`

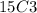
Number of ways to pick 2 girls from 10:

`10C2`

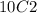
Therefore, the number of ways the choice can be made will be:

`\begin{gathered} \Rightarrow15C3*10C2=455*45 \\ =20475\text{ ways} \end{gathered}`

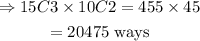
QUESTION II

If a particular boy is included, the number of choices will then become:

`14C2`

Therefore, the number of ways the choice can be made will be:

`\begin{gathered} \Rightarrow14C2*10C2=91*45 \\ =4095\text{ ways} \end{gathered}`

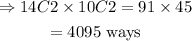
QUESTION III

If a particular girl is excluded, the number of choices will be: