Given
Length = 3 inches , dl/dt = 1 inch/minute
width = 2 inches , db/dt = -0.5 inch/minute
Find
Is the area increasing or decreasing?
Step-by-step explanation
as we know , area = length * breadth
so ,

differentiate with respect to t.
so ,
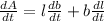
now substitute the values,
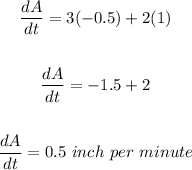
therefore , area is increasing at the rate of 0.5 inch per minute
Final Answer
Hence , the area is increasing at the rate of 0.5 inch per minute.