Given that the predicted value is 227 while the actual value is 250.
1.
The difference is calculated as,
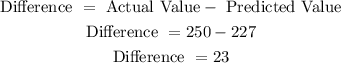
Thus, the difference is 23.
2.
Consider the equation,
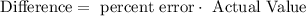
Substitute the values,
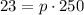
This is the required equation.
3.
Solve the equation obtained above for the variable 'p' as,
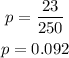
Thus, the value of 'p' is obtained as 0.092.
4.
The value of 'p' in percentage can be obtained as,
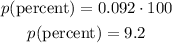
Thus, the value of percentage error is 9.2%.