We are given the following polynomial function

We are asked to list the zeros of the function according to the behavior of the graph.
Zeros where the graph crosses the x-axis:
The graph crosses the x-axis at these points
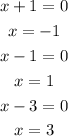
So, there are three zeros where the graph crosses the x-axis.
-1, 1, 3
Zero(s) where the graph touches but does not cross the x-axis:
There is no such zero there touches the x-axis but does not cross it.
Find the y-intercept of the graph:
The y-intercept is the point where the graph crosses the y-axis.
Substitute x = 0 into the function to find the y-intercept.
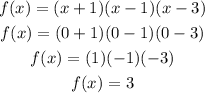
So, the y-intercept of the graph is 3