So we have to find the limit when x tends to 3 of:
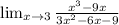
For this purpose we can use the L'Hôpital's rule. It states that when the limits of f(x) and g(x) are equal to 0 or ±∞, f and g are differentiable in an interval around a number x=c, and g'(x) is not zero then we have:
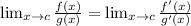
In this case, our function is composed of two functions. Let's see if we can apply the rule to them:
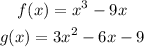
Let's check their limits when x tends to 3:
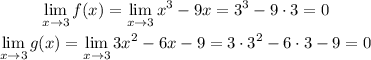
They are polynomials so they are differentiable in any real interval and g'(x) is not always zero:
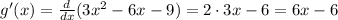
So they meet the conditions and we can apply the L'Hôpital's rule:
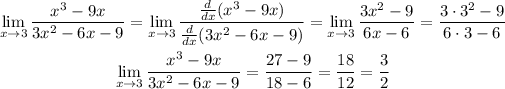
So the limit we were looking for is 3/2. Then the answer is the fourth option.