In the formula S = 180(n-2), the number of sides of the polygon is represented with the variable n.
A) The figure has 3 sides.
Therefore, we will substitute n = 3 into the equation and solve for S.
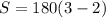
Simplify the equation to get:
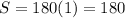
The figure has 3 sides so the sum of angles is 180 degrees.
B) The figure has 4 sides.
Therefore, we will substitute n = 4 into the equation and solve for S.
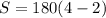
Simplify the equation to get:
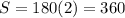
The figure has 4 sides so the sum of angles is 360 degrees.
SOLVING FOR X:A)
Now that we know the sum of the angles is equal to 180 degrees, we can add all of the angles in the figure and set them equal to 180.
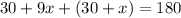
Now, we have an equation where we can solve for x.
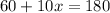
Subtract 60 from both sides.
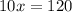
Divide both sides by 10.
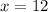
The value of "x" in the first figure (Part A) is equal to 12.
B)
We know that the angles add up to 360 in this figure, so let's create an equation and set it equal to 360.
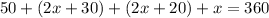
Combine like terms to simplify the equation.

Subtract 100 from both sides.

Divide both sides by 5.
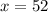
The value of "x" in the second figure (Part B) is equal to 52.