Which of the graphs represents the line with the following slope and y-intercept:m = (1)/(2) \: b = - 2

Question

which of the graphs represents the line with the following slope and y-intercept:
`m = (1)/(2) \: b = - 2`

Answer 1

`\begin{gathered} m=(1)/(2) \\ b=-2 \end{gathered}`

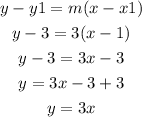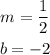
The equation of the line in the slope-intercept form is given by:

`\begin{gathered} y(x)=mx+b \\ so\colon \\ y(x)=(1)/(2)x-2 \end{gathered}`

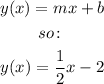
The graph of this line is given by:

----

`\begin{gathered} y=mx+b \\ (-4,0) \\ (0,3) \\ m=(3-0)/(0-(-4))=(3)/(4) \end{gathered}`

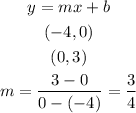
so, using the point slope equation:

`\begin{gathered} y-(0)=(3)/(4)(x-(-4)) \\ y=(3)/(4)(x+4) \\ y=(3)/(4)x+3 \end{gathered}`

-----------------------------------

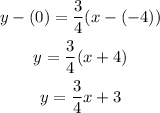
Let:

`\begin{gathered} y=3x+2 \\ m1=3 \end{gathered}`

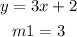
If 2 lines are parallel, then:

`m1=m2`

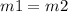
where m2 is the slope of the other line, so:

`\begin{gathered} m2=3 \\ let\colon \\ (x1,y1)=(1,3) \end{gathered}`

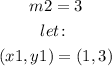
Using the point-slope equation:

`\begin{gathered} y-y1=m(x-x1) \\ y-3=3(x-1) \\ y-3=3x-3 \\ y=3x-3+3 \\ y=3x \end{gathered}`