The given equation is:
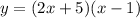
We need to transform it into the form:

We can do it by multiplying the parentheses:
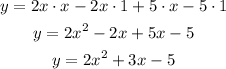
Then a=2, b=3 and c=-5.
The vertex of the parabola is given by (h,k) where:
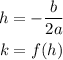
Then h and k are equal to:
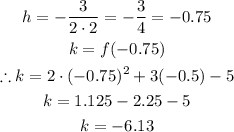
Thus, the vertex is at (-0.75, -6.13).
Now, to find the zeros of the function, we can use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
By replacing the know values we obtain:
![\begin{gathered} x=\frac{-3\pm\sqrt[]{3^2-4(2)(-5)}}{2(2)} \\ x=\frac{-3\pm\sqrt[]{9+40}}{4} \\ x=\frac{-3\pm\sqrt[]{49}}{4} \\ x=(-3\pm7)/(4) \\ \text{Then x is equal to:} \\ x=(-3+7)/(4)=(4)/(4)=1\text{ and }x=(-3-7)/(4)=(-10)/(4)=-2.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/osujbb9mkz3jqmvv5mo5dqj4idr4llpxav.png)
Thus, the zeros are at: (-2.5,0) and (1,0).
Answer: the graph that represents the parabola is the last one with the vertex at (-0.75, -6.13) and the zeros at (-2.5,0) and (1,0).