Question

The expression u^2+ 20u + 100 in factored form is…

Answer 1

Given the expression:

`u^2+20u+100`

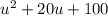
To factor the given expression, we need two numbers the product of them = 100 and the sum of them = 20

We will factor the number 100

100 = 1 x 100 ⇒ 1 + 100 = 101

100 = 2 x 50 ⇒ 2 + 50 = 52

100 = 4 x 25 ⇒ 4 + 25 = 29

100 = 5 x 20 ⇒ 5 + 20 = 25

100 = 10 x 10 ⇒ 10 + 10 = 20

So, the suitable numbers are 10, 10

so, the factorization will be as follows:

`u^2+20u+100=(u+10)(u+10)=(u+10)^2`

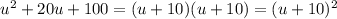
The given expression is a complete square.

So, the answer will be (u+10)(u+10)

Or can be written as (u+10)²