Question

the area of triangle abc is 5m squared. what is the area of the image of triangle abc after a dilation by a scale factor of k=3

Answer 1

We have a triangle ABC with area of 5 m².

We have to calculate the area of the image triangle after a dilation of ABC by a scale factor of k = 3.

When we dilate a figure in the xy-plane with scale factor k, the sides will have a length that is k times the length of the pre-image corresponding sides.

The area of the image, as it is a product of the image sides, will be k² times the area of the pre-image.

Then, we can calculate the area of the image as:

`\begin{gathered} A_{\text{image}}=k^2\cdot A_{\text{preimage}} \\ A_{\text{image}}=3^2\cdot5m^2 \\ A_{\text{image}}=9\cdot5m^2 \\ A_{\text{image}}=45m^2 \end{gathered}`

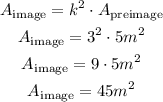
Answer: the area of the image triangle will be 45 m².