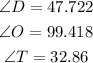Please answer #12 as seen in the picture. Thank you.

Question

asked Sep 27, 2023 44.4k views

1 Answer

Pavlo Zhukov · Answer 1 · 2023-10-03T16:42:32+0000

If we choose a=20, b=15 and c=11 ans substitute these values into the given formula, we have

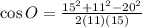
$\cos O=(15^2+11^2-20^2)/(2(11)(15))$

which gives

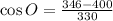
$\cos O=(346-400)/(330)$

then

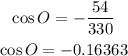
$\begin{gathered} \cos O=-(54)/(330) \\ \cos O=-0.16363 \end{gathered}$

which gives

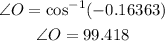
$\begin{gathered} \angle O=\cos ^(-1)(-0.16363) \\ \angle O=99.418 \end{gathered}$

Once we have one angle, we can use the law of sines as follows,

$(\sin O)/(20)=(\sin D)/(15)$

which gives

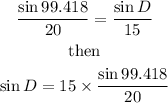
$\begin{gathered} (\sin 99.418)/(20)=(\sin D)/(15) \\ \text{then} \\ \sin D=15*(\sin99.418)/(20) \end{gathered}$

so, angle D is

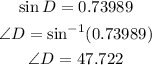
$\begin{gathered} \sin D=0.73989 \\ \angle D=\sin ^(-1)(0.73989) \\ \angle D=47.722 \end{gathered}$

Finally, since the interior angles of any triangle add up to 180, we have

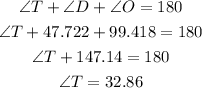
$\begin{gathered} \angle T+\angle D+\angle O=180 \\ \angle T+47.722+99.418=180 \\ \angle T+147.14=180 \\ \angle T=32.86 \end{gathered}$

In summary, the answers are:

$\begin{gathered} \angle D=47.722 \\ \angle O=99.418 \\ \angle T=32.86 \end{gathered}$