Step 1: Write out the formula
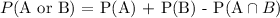
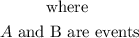
Step 2: Write out the given values and substitute them into the formula
Let A be the event of "shopper reads the newspaper 1-2 times.
and
Let B be the event of "shopper remembered 1-3 cards".
n(A) = 15 + 10 = 25
n(B) = 8 + 15 = 23
n(U) = 8 + 15 + 9 + 10= 42
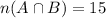
Therefore,
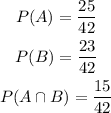
Hence,
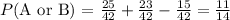
Thus the probability that a randomly selected shopper reads the newspaper 1-2 times a week or remembered 1-3 cards is 11/14