Question

A man has a box of coins that he uses when playing poker with friends. The box currently contains 48 coins, consisting of pennies, dimes, and quarters. The number of pennies is equal to the number of dimes, and the total value is $4.98. How many of each denomination of coins does he have?Let x represent the number of pennies. Complete the table (please see attached)

Answer 1

Given:

Let the number of quarters coins be represented by y

`\begin{gathered} Total\text{ coins is 48} \\ x+x+y=48 \\ 2x+y=48..............................(1) \end{gathered}`

The penny coin is worth one cent or $0.01

A dime is worth 10 cents or $0.10

The quarter is an American coin worth 25 cents or $0.25

The total value of the coins is;

`\begin{gathered} 0.01x+0.1x+0.25y=4.98 \\ 0.11x+0.25y=4.98..................................(2) \end{gathered}`

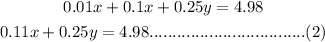
From equation (1);

`y=48-2x.................................(3)`

Substituting equation (3) into equation (2);

`\begin{gathered} 0.11x+0.25(48-2x)=4.98 \\ 0.11x+12-0.5x=4.98 \\ 12-4.98=0.5x-0.11x \\ 7.02=0.39x \\ (7.02)/(0.39)=x \\ x=18 \end{gathered}`

Substituting the value of x gotten into equation (3);

`\begin{gathered} y=48-2(18) \\ y=48-36 \\ y=12 \end{gathered}`

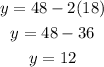
Therefore,

The number of pennies = 18 coins

The number of dimes = 18 coins

The number of quarters = 12 coins