Question

Jada is standing 10 feet from the base of a tree and spots a nest sitting on a branch. the angle of elevation from the ground where she is standing to the nest is 55 degrees. find the height of the nest to the nearest tenth

Answer 1

14.3 ft

Step-by-step explanation:

We can represent the situation as:

Now, we can relate the measure of the angle, the height x, and the distance 10 ft using the trigonometric function tangent as:

`\begin{gathered} \tan 55=(Opposite)/(Adjacent) \\ \tan 55=(x)/(10) \end{gathered}`

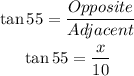
So, solving for x, we get:

`\begin{gathered} 10\cdot\tan 55=10\cdot(x)/(10) \\ 10\cdot\tan 55=x \\ 10\cdot1.43=x \\ 14.3\text{ ft = x} \end{gathered}`

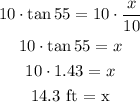
Therefore, the height of the nest to the nearest tenth is 14.3 ft.