Question

The height of a triangle is 6 cm longer than its base. If its area is 36 square cm, what is the length of the base and the height?

Answer 1

Given:

There are given that the height of a triangle is 6 cm longer than its base.

Step-by-step explanation:

According to the question.

We need to find the length of the base and the height.

So,

Suppose the height of the triangle is H and the base of the triangle

According to the given data:

`H=B+6`

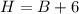
Then,

From the area of the triangle:

`A=(1)/(2)(B* H)`

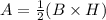
Then,

Put all the value into the give formula:

So,

`\begin{gathered} A=(1)/(2)(B* H) \\ 36*2=(1)/(2)*2* B(B+6) \\ B^2+6B=72 \end{gathered}`

Then,

`\begin{gathered} B^(2)+6B=72 \\ B^2+6B-72=72-72 \\ B^2+6B-72=0 \end{gathered}`

Then,

`\begin{gathered} B^(2)+6B-72=0 \\ (B+12)(B-6)=0 \\ B=-12;B=6 \end{gathered}`

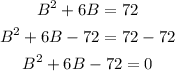
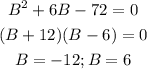
Then,

According to the concept, the value of the base cannot be negative.

So,

The value of the base is:

`B=6`

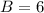
Now,

From the give statement:

`\begin{gathered} H=B+6 \\ H=6+6 \\ H=12 \end{gathered}`

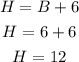
Final answer:

Hence, the base of the triangle is 6 and the height of the triangle is 12.