Question

A large crate of puzzle pieces is at rest at the top of a steep incline with an angle of 35 degrees. The crate is then released from rest. The coefficient of kinetic friction between the crate and the incline is 0.42. How fast is the crate moving at the bottom of the incline if it takes 2.5 seconds to reach the bottom? If the ground at the bottom of the incline is level and the coefficient of kinetic friction between the crate and ground is 0.68, how far from the bottom of the incline does the crate travel?

Answer 1

Force diagram:

To calculate the velocity of the box at the bottom of the ramp, we will need to use kinematics.

For kinematic formulas, we will need to find the acceleration the box feels. We can solve this by finding net force

∑Fx = Fgx - Ff --> net force in the horizontal direction = force of gravity in the horizontal direction - force of friction

∑Fx = mg(sin(35)) - mg cos 35 (.42)

ma = mg(sin(35)) - mg cos 35 (.42)

a = g(sin(35)) - g cos (35) (.42)

a = 2.249 m/s^2

Now we can use the kinematic formulas

a = 2.249 m/s^2

t = 2.5 seconds

inital velocity = 0 m/s

final velocity = ? m/s

We can use the formula to find final speed

`v_f=v_0+at`

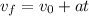
vf = 0 + 2.5(2.249) = 5.6235 m/s

The next part requires us to find the distance the box travels

To do this, we can use the formula

`d=(v^2)/(2\mu g)`

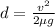
v = 5.6235 m/s

μ = .68

g = 9.8 m/s^2

d = (5.6235)^2/2(.68)(9.8) = 2.37 meters