Question

A 42Inch suggests that the main diagonal of the is 42 inches Determine the dimensions of the screen a 42 inch TV with a 4 3 aspect ratio

Answer 1

The dimensions are 33.6 and 25.2 inches.

Step-by-step explanation:

Let's say the screen is a rectangle with sides "x" and "y".

We know that x/y = 4/3. So, x = (4/3)y

Since the diagonal is known, we can represent the tv as:

The measures of x and y can be found using the green part of the figure. As we can see, we have a triangle rectangle.

The hypothesis of the triangle is 42 and the sides y and (4/3)y.

Using the Pythagorean Theorem, we know that:

`\text{hyp}^2=a^2+b^2`

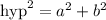
where "hyp" is the hypotenuse and a and b the sides.

So,

`\begin{gathered} 42^2=((4)/(3)y)^2+y^2 \\ 1764=(16)/(9)y^2+y^2 \\ 1764=(16y^2+9y^2)/(9) \\ 1764=(25y^2)/(9) \\ 1764\cdot9=25y^2 \\ (15876)/(25)=y^2 \\ y^2=635 \\ y=\pm25.2\text{ } \\ \text{ Since y is a positive a measurement, } \\ y=25.2\text{ inches} \end{gathered}`

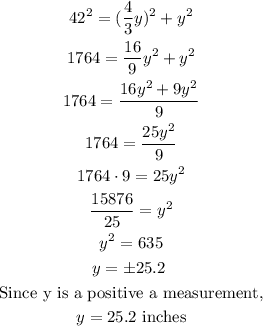
Also, since x = (4/3)y:

`\begin{gathered} x=(4)/(3)y \\ x=(4)/(3)\cdot25.2 \\ x=33.6\text{ inches} \end{gathered}`

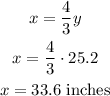
Thus, the dimensions of the screen are 25.2 and 33.6 inches.