We will have the following:
First, we determine the equation for the slope, that is:
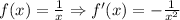
Now, to determine the average slope we examine the slopes at the edges:

So, the average slope will be given by:
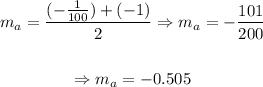
So, the average slope in that interval is -0.505.
Now, we determine the exact point where the slope is that, that is:
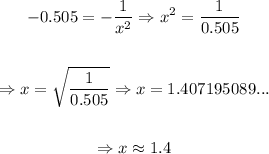
So, the exact point is sqrt( 1 / 0.505), that is approximately 1.4.