SOLUTION
Let the weight of the large box be x
Let the weight of the small box be y
Since the combined weight of the boxes is 90 it follows:
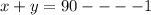
The number of small boxes are 65 and the number of large boxes are 70 and the combined total pounds is 6025
This gives
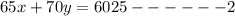
Solve the equation
Frrom equation 1
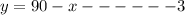
Substitute y=90-x into equation 2
This gives
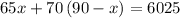
Solve the equation
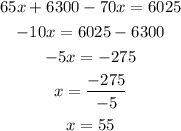
Substitute x=55 into equation 3
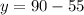
Calculate the value
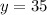
Therefore the weight of the large box is 55
The weight of the small box is 35