Question

The Enterprise wants to orbit a4.15 x 10^24kg planet with a period of14100 s. What should the radius oftheir orbit be?

Answer 1

Given:

Mass of planet, m = 4.15 x 10²⁴ kg.

Period, T = 14100 s

Let's find the radius.

To find the radius, apply the formula from Kepler's Third aw:

`\begin{gathered} (T^2)/(R^3)=(4\pi^2)/(GM) \\ \\ \end{gathered}`

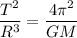
Where R is the radius.

Rewrite the formula for r:

`R=\sqrt[3]{(GM*T^2)/(4\pi^2)}`

Where:

G is gravitational constant = 6.67 x 10⁻¹¹ m3 kg-1 s-2

M is the mass = 4.15 x 10²⁴ kg

T is the period = 14100 s

π = 3.54

Plug in values and solve for R;

`\begin{gathered} R=\sqrt[3]{(6.67*10^(-11)*4.15*10^(24)*14100^2)/(4\pi^2)} \\ \\ R=\sqrt[3]{(5.503*10^(22))/(39.4784)} \\ \\ \end{gathered}`

Solving further:

`\begin{gathered} R=\sqrt[3]{1.394*10^(21)} \\ \\ R=11170796.49\approx1.12*10^7\text{ m} \end{gathered}`

Therefore, the orbital radius will be 1.12 x 10⁷ meters.

ANSWER:

1.12 x 10⁷ m