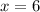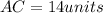Question

I need help with this problem. I don’t understand it. The question is. The value of x is ___The length of AC is ___

Answer 1

Given:

ABCD is isosceles trapezoid.

AC=3x-4 and BD=x+8 are the diagonals of the given trapezoid.

Required:

We need to find the value of x and the length of AC.

Step-by-step explanation:

Recall that the diagonals of an isosceles trapezoid have the same length

`AC=BD`

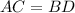
Substitute AC=3x-4 and BD=x+8 in the equation to find the value of x.

`3x-4=x+8`

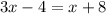
Add 4 to both sides of the equation.

`3x-4+4=x+8+4`
`3x=x+12`

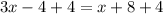
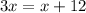
Subtract x from both sides of the equation.

`3x-x=x+12-x`
`2z=12`

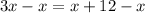
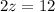
Divide both sides of the equation by 2.

`(2x)/(2)=(12)/(2)`
`x=6`

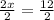
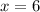
We get x =6 and substitute x =6 in the equation AC=3x-4 to find the length of AC.

`AC=3(6)-4`
`AC=14units`

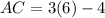
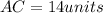
Final answer:

`x=6`
`AC=14units`