Given:
The function is
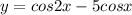
Required:
To find the points at which the tangent equations to the graph of the following functions are parallel to the x-axis.
Step-by-step explanation:
Differentiate the given function.

Given that tangent to the curve is parallel to the x-axis.
So the slope of the tangent = Slope of X-axis
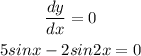
Use the identity
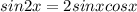
Now
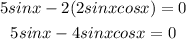
Take out common sinx
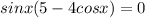
![undefined]()