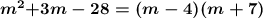One method to factor a trinomial in its standard form is the X-box method.
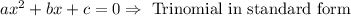
The first step for this method is to multiply a and c and place ac at the top:
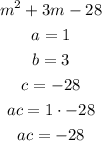
The second step is to place b at the bottom:
The third step is to find two numbers that multiply to the top number ac and add to the bottom number b. For this, we can use the factors of -28. The factors of -28 are 1,2,4,7,14,28,-1,-2,-4,-7,-14, and -28.

As we can see, the factors of -28 that serve us are -4 and 7 because multiplied they give as a result -28 and added they give as a result 3.
Finally, we can write the initial trinomial in its factored form using the two middle numbers from the third step.