We need to find the values for theta (0 ≤ theta ≤ 2pi) given the next equation:
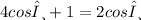
Let us solve theta:
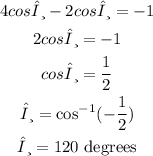
Now, we need to convert 120 degrees to radians:
We have that the interval is 2π = 360 degrees.
Hence, 2*120 = 240 degrees is still on the interval.
Convert 240 degrees to radians:
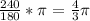
Therefore, the result is (2π/3, 4π/3)
The correct answer is the first option.