Question

identify each classification of the real number system that can describe the set of numbers shown {-√36, 35%, 2}) Whole) Integer) Real) Natural) Irrational) Rational

Answer 1

The classifications that can describe the set of numers is:

Real

Rational

To solve this, let's convert all numebers to decimal:

`-\sqrt[]{36}=-6`

35% = 35/100 = 0.35

Then the set is:

{-6, 0.35, 2}

Let's see the options:

Whole can't be because there is a negative number and a decimal number.

Integer can't be because there's a decimal number.

Real can be used because those are all real numbers.

Natural can't be because there is a negative number and a decimal number.

Irrational can't be, because those are all rational numbers

Rational can be used, because all those numbers can be written as a fraction:

`\begin{gathered} -6=-(6)/(1) \\ 0.35=(35)/(100) \\ 2=(2)/(1) \end{gathered}`

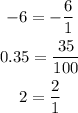
Then, the only classifications that could be used are Real and Rational