Question

Kaia rolled a number cube 50 times Outcome Rolled: 1, 2, 3, 4, 5, 6Number of Rolls: 10, 11, 10, 6, 8, 5* round to the nearest thousandth A) assuming the cube is fair, compute the theoretical probability of rolling a 1 or 5B) From Kaia's results, compute the experimental probability of rolling a 1 or 5

Answer 1

Given:

The table given above is done based on experimental probability.

Question a:

The theoretical probability:

Assuming the cube is fair, the each side has 1 outcome, meaning the total outcome is 6.

Hence,

The theoretical probability of rolling a 1 or 5 is;

`\begin{gathered} P(1\text{ or 5)= P(1) + P(5)} \\ =(1)/(6)+(1)/(6) \\ =(2)/(6) \\ =(1)/(3) \\ =0.333333 \\ \\ To\text{ the nearest thousandth,} \\ P(1\text{ or 5)= }0.333 \end{gathered}`

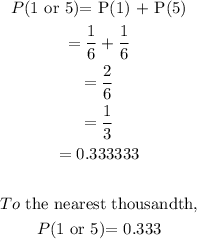
Therefore, the theoretical probability of rolling a 1 or 5 to the nearest thousandth is 0.333

Question b:

The experimental probability:

The experimental probability of rolling a 1 or 5 is from the table given,

`\begin{gathered} n\text{umber of 1 rolled=10} \\ n\text{umber of 5 rolled=8} \\ \text{Total outcome from the experiment=50} \\ \\ P(1\text{ or 5)= P(1) + P(5)} \\ =(10)/(50)+(8)/(50) \\ =(18)/(50) \\ =0.36 \\ \\ To\text{ the nearest thousandth,} \\ P(1\text{ or 5)=}0.360 \end{gathered}`

Therefore, the experimental probability of rolling a 1 or 5 to the nearest thousandth is 0.360

Question c:

From the probability of both values gotten from the theoretical and experimental, we can see that the difference is small.

Therefore, the true statement assuming that the cube is fair is;