Question

Last year, Debra had $10,000 to invest. She invested some of it in an account that paid 6% simple interest per year, and she invested the rest in an accountthat paid 8% simple interest per year. After one year, she received a total of $720 in interest. How much did she invest in each account?

Answer 1

Given :

Amount to be invested = $ 10,000

rate of first account = 6%

rate of second account = 8%

Total amount she received on interest = $720

Solution

Let the amount she invested in the first account be x

Let the amount she invested in the second account be y

Then,

`x\text{ + y = 10 000}`

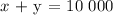
Also, using the simple interest formula:

`S\mathrm{}I\text{ = }(P* R* T)/(100)`

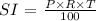
We can express the second and last statements mathematically

`\begin{gathered} \frac{x\text{ }*\text{ 6}*1}{100}\text{ + }\frac{y\text{ }*\text{ 8 }*\text{ 1}}{100}\text{ = 720} \\ re-\text{arranging} \\ 6x\text{ + 8y = 72000} \end{gathered}`

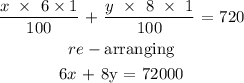
We can solve the equations simultaneously to obtain x and y

`\begin{gathered} x\text{ + y = 10000} \\ 6x\text{ + 8y = 72000} \\ x\text{ = 4000} \\ y\text{ = 6000} \end{gathered}`

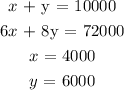
She invested $4000 and $6000 respectively.