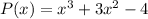The equation that represents the 3rd degree polynomial shown on the graph is obtained as follows:
- Because the curve "touches" the x- axis at one point where x = -2, and it "crosses" the x-axis at the point where x = 1, this means that there are two roots at x = -2 and just one root at x = 1.
Therefore, the equation of the polynomial can be generally represented as:

Now, we need to find the value of the constant A.
To do this simply, we have to look at the y-intercept of the curve. That is, the point where the curve crosses the y-axis. The coordinate of this point is (0, -4), as seen on the graph.
This means that when x = 0, y = -4. We substitute these values into the general equation we obtained earlier, as follows:

Simplifying the above gives:
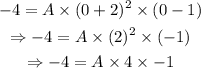
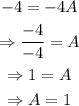
Therefore, we can say that the equation that represents the polynomial shown on the graph is :
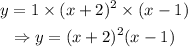
Final simplification gives:

Since we are asked to express the polynomial equation in the form of P(x), we can therefore write it as follows: