Question

Use the intermediate theorem (Roll's) to show that f(x)=x^3-3x + 2x + 1 has a root on the interval (-2,3).

Answer 1

Given the function

`f(x)=x^3-3x+2x+1`

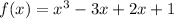
then we use the intermediate theorem for the given interval

`\begin{gathered} f(x)=x^3-x+1 \\ f(-2)=(-2)^3-(-2)+1=-8+2+1=-5 \\ f(3)=(3)^3-3+1=27-3+1=25 \end{gathered}`

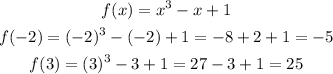
So the question now is to show that for at least one number c in [-2,3] we get:

`f(c)=0`

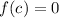
Then, f is continuous on [-2,3] because it is a polynomial and they are continuous everywhere.

`\begin{gathered} f(-2)=-5 \\ and \\ f(3)=25 \end{gathered}`

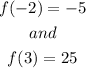
0 is between f(-2) and f(3), so by the intermediate value theorem, there is at least one number c in [-2,3] for which f(c)=0.

That is, the original equation has a solution.