shortest side: 851
middle side:927
longest side : 1306
Step-by-step explanation
Step 1
Let
x represents the shortest side
y represents the middle side
z represents the longest side
so, set the equations
a) the perimeter of a rectangle is the sum of the sides, so
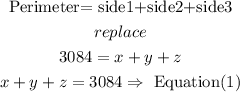
b) The shortest side measures 76 mi less than the middle side( in other words, you have to subtract 76 from middle side to get the shortest side)
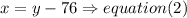
c) and the longest side measures 379 mi more than the middle side,( in other words, you have to add 379 to middle side to obtain the longest side)
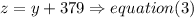
Step 2
solve the equations
a) now, replace the x an z value sfrom equation (2) and (3) into equation(1)
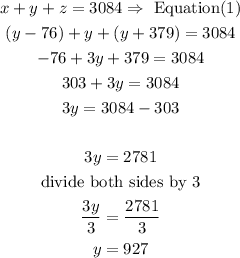
now, replace the y value in equatino (2) to find x
b)
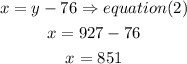
c) finally, prelace x and y value in equation (1) to find z
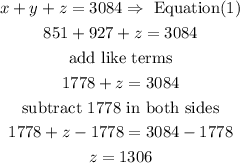
so
shortest side: 851
middle side:927
longest side : 1306
I hope this helps you