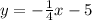Question

Through: (-4,-4), perpendicular to y=4x-2

Answer 1

First let's determine the slope of the straight line

A perpendicular line fulfills the following relationship

`m1m2=-1`

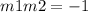
Where

m1 = slope of the first straight line

m2 = slope of the perpendicular straight line

`\begin{gathered} 4m2=-1 \\ m2=-(1)/(4) \end{gathered}`

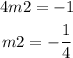
Now we are going to calculate the intersection point

`\begin{gathered} b=y-mx \\ b=-4-(-(1)/(4))\cdot(-4) \\ b=-4-1 \\ b=-5 \end{gathered}`

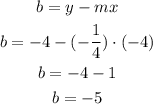
The equation of the line that passes through the point (-4,-4) with a slope of -1/4

`y=-(1)/(4)x-5`