Question

Two boats, 70m apart and on opposite sides of a light-house are in straight line with the light house. The angles of elevation of the top of the light-house from the two boats are 70° and 42°. Find the height of the light-house.

Answer 1

A diagram of the problem will be:

Where h is the height of the light-house.

We can apply tangent to find the height.

Let's start:

`\begin{gathered} \tan42=(h)/(70-x) \\ \\ h=\tan42*(70-x)\text{ Equation 1} \\ \\ \tan70=(h)/(x) \\ \\ h=\tan70*x\text{ Equation 2} \end{gathered}`

Now, find h in terms of x from equation 2, and replace it into equation 1, to find x:

`\begin{gathered} h=2.75x \\ 2.75x=tan42(70-x) \\ 2.75x=0.9(70-x) \\ 2.75x=0.9*70-0.9x \\ 2.75x=63-0.9x \\ 2.75x+0.9x=63 \\ 3.65x=63 \\ x=(63)/(3.65) \\ x=17.26m \end{gathered}`

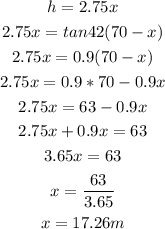
Now, replace x into equation 2 and solve for h:

`\begin{gathered} h=tan70*x \\ h=2.75*17.26m \\ h=47.42m \end{gathered}`

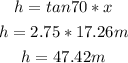
The height of the light-house is 47.42 m.