Question

Unless specifically stated otherwise, you may assume the speed of sound for all the scenarios below is 350 m/s.5.A particular star usually emits infrared light with a frequency of 900 GHz (900 x 109 Hz). An infrared telescope observes the star to have emit a frequency of 820 GHz. How fast is the star moving relative to earth and in what direction? (Recall that infrared waves move at the speed of light 3.00 x 108 m/s)

Answer 1

Given:

The frequency emitted by the source, f_s=900 GHz

The observed frequency, f=820 GHz

To find:

The speed of the source and the direction of motion of the source.

Step-by-step explanation:

The change in the frequency is given by,

`\Delta f=f_s-f`

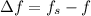
On substituting the known values,

`\begin{gathered} \Delta f=900\text{ GHz}-820\text{ GHz} \\ =80\text{ GHz} \end{gathered}`

Thus the change in the frequency is positive. That is the frequency is decreasing. This is called a redshift and the star is moving away from the earth.

The speed of the source is given by the equation,

`f=f_s*(c)/(c+v)`

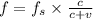
Where c is the speed of light and v is the speed of the source.

On substituting the known values,

`\begin{gathered} 820*10^9=900*10^9*(3*10^8)/(3*10^8+v) \\ \implies v=(900*10^9*3*10^8)/(820*10^9)-3*10^8 \\ =29.3*10^6\text{ m/s} \end{gathered}`

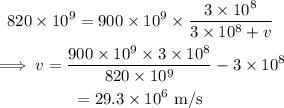
Final answer:

The velocity of the star is 29.3×10⁶ m/s

And the star is moving away from the earth.