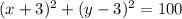Given:
The endpoints of the diameter of a circle are located at (3,-5) and (-9, 11).
To find the equation of the circle, we need the coordinates of the vertex and the length of the radius.
We will use the given points to find the length of the diameter = d
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt[]{(3+9)^2+(11+5)^2}=\sqrt[]{400}=20](https://img.qammunity.org/2023/formulas/mathematics/college/cnnfc79ky97lpbcz7l7k9kbc1uq3z17s6k.png)
The radius = r = 0.5 * d = 0.5 * 20 = 10
The center of the circle is the midpoint of the diameter
So,
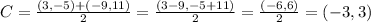
the equation of the circle has the following form:

Where: r is the radius and center = ( h, k )
So,
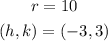
The equation of the circle will be: