Question

9) Malick has $235. He has one less than three times as many $10 bills than $5 bills. Find how many of each bill that he has.

Answer 1

7 bills of $5 and 20 bills of $10

Step-by-step explanation

Step 1

Let

Malick has $235=total = 235

total=235

number of bill $5= x

number of bill $10=y

He has one less than three times as many $10 bills than $5 bills=

3x=y+1

`3x=y+1\text{ Equation (1)}`

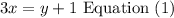
Step 2

the total is 235, so

total for $ 5 bills= 5* number of bills $5=5x

total for $ 10 bills= 10* number of bills $10=10x

`5x+10y=235\text{ Equation(2)}`

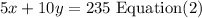
Step 2

using equation (1I and (2) solve for x and y

`\begin{gathered} 3x=y+1 \\ 5x+10y=235 \end{gathered}`

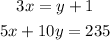
isolate, y in equation (1)

`\begin{gathered} 3x=y+1 \\ \text{divide each side by 3} \\ (3x)/(3)=(y)/(3)+(1)/(3) \\ x=(y)/(3)+(1)/(3) \end{gathered}`

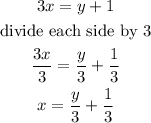
replace the value of x in equation (2)

`\begin{gathered} 5x+10y=235 \\ 5((y)/(3)+(1)/(3))+10y=235 \\ (5y)/(3)+(5)/(3)+10y=235 \\ y((5)/(3)+\frac{10}{})=235-(5)/(3) \\ \\ y((35)/(3))=233.33 \\ y=(233.33\cdot3)/(35) \\ y=20 \end{gathered}`

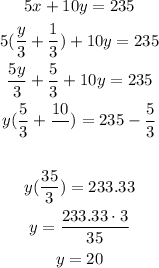
replace the value of y in equation (1) to fin d x

`\begin{gathered} 3x=y+1 \\ 3x=20+1 \\ 3x=21 \\ \text{divide by 3} \\ (3x)/(3)=(21)/(3) \\ x=7 \end{gathered}`

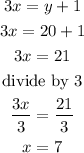
so, the answer is

7 bills of $5 and 20 bills of $10