Question

The wilson family was one of the first to come to the U.S. they had 4 children . Assuming that the probability of a child being a girl .5, find the probability that the Wilson family had: at least 3 girls at most 2 girls

Answer 1

P( at least 3 girls) = 0.3125

P( at most 2 girls) = 0.6875

Step-by-step explanation:

To know the probability that the Wilson family had at least 3 girls, we will use the binomial distribution because we have n identical events with a probability p of success and probability (1 - p) of fail.

In this case, n is the number of children and we consider success if they have a girl, so p is 0.5 and (1-p) is also 0.5 because:

1 - p = 1 - 0.5 = 0.5

Then, the probability to have x number of girls can be calculated as:

`P(x)=\text{nCx}\cdot p^x\cdot(1-p)^(n-x)`

Where nCx is equal to:

`\text{nCx}=(n!)/(x!(n-x)!)`

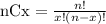
Now, the probability that the Wilson family had at least 3 girls is the probability to have 3 girls added to the probability to have 4 girls, so:

`P(x\ge3)=P(3)+P(4)`

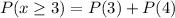
Where P(3) and P(4) are equal to:

`\begin{gathered} P(3)=4C3\cdot0.5^3\cdot0.5^1=(4!)/(3!(4-3)!)\cdot0.5^3\cdot0.5^1=0.25 \\ P(4)=4C4\cdot0.5^4_{}\cdot0.5^0=(4!)/(4!(4-4)!)\cdot0.5^3\cdot0.5^1=0.0625 \end{gathered}`

Therefore, the probability that the Wilson family had at least 3 girls is equal to:

`P(x\ge3)=0.25+0.0625=0.3125`

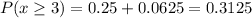
In the same way, the probability that the Wilson family had at most 2 girls can be calculated as:

`P(x\leq2)=P(0)+P(1)+P(2)`
`\begin{gathered} P(0)=4C0\cdot0.5^0\cdot0.5^4=0.0625 \\ P(1)=4C1\cdot0.5^1\cdot0.5^3=0.25 \\ P(2)=4C2\cdot0.5^2\cdot0.5^2=0.375 \end{gathered}`
`P(x\leq2)=0.0625+0.25+0.375=0.6875`

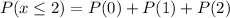
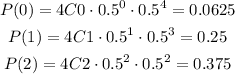
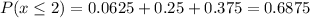
Therefore, the answers are:

P( at least 3 girls) = 0.3125

P( at most 2 girls) = 0.6875