Since the triangle is a regular triangle i.e the triangle is an Equilateral triangle in which all sides and angles are equal.
Let us start by sketching the image of the regular triangles with some information required.
Let us now bring out the internal triangle and solve for x
Using Cosine of angle to solve for x
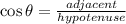
Where,

Therefore,
![\begin{gathered} \cos 30^0=(x)/(6) \\ \therefore x=6\cos 30^0=6*\frac{\sqrt[]{3}}{2}=3\sqrt[]{3} \\ \therefore x=3\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i7wayp7dgzeqj0av7gmsdgsgz8xogvzykz.png)
Hence, one side of the triangle will be
![3\sqrt[]{3}+3\sqrt[]{3}=6\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/ejkvl4hxdvzgjwo8up053z438j7istczj3.png)
Recall: The triangle is a regular triangle, therefore all sides are equal.
Solving for the perimeter of the triangle
The perimeter of the triangle will be the sum of all three sides.
Therefore,
![6\sqrt[]{3}+6\sqrt[]{3}+6\sqrt[]{3}=18\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/ksthdalxiuxk06016jyr5npny0y2veqswx.png)
Hence, the perimeter of the regular triangle is,
![18\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/q3da9qp655asqs4wqwb7su00a69isl8ng6.png)
Let us now solve for the area(A) of the triangle.
Heron's formula is used to find the area of a triangle that has three different sides. Heron's formula is written as, Area = √[s(s-a)(s-b)(s-c)], where a, b and c are the sides of the triangle, and 's' is the semi perimeter of the triangle.
Where,
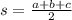
Here a, b, and c are equal.
Hence,
![\begin{gathered} s=\frac{6\sqrt[]{3}+6\sqrt[]{3}+6\sqrt[]{3}}{2}=\frac{18\sqrt[]{3}}{2}=9\sqrt[]{3} \\ \therefore s=9\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/17joslzf6890mmwnu1isfcyenkgcdhbc2q.png)
Therefore, the area will be
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
![\begin{gathered} A=\sqrt[]{9\sqrt[]{3}(9\sqrt[]{3}-6\sqrt[]{3})(9\sqrt[]{3}-6\sqrt[]{3}(9\sqrt[]{3}-6\sqrt[]{3})} \\ A=\sqrt[]{9\sqrt[]{3}(3\sqrt[]{3})(3\sqrt[]{3})(3\sqrt[]{3})}=\sqrt[]{9*3*3*3(\sqrt[]{3*3*3*3})} \\ A=\sqrt[]{243\sqrt[]{81}}=\sqrt[]{243*9}=\sqrt[]{2187}=27\sqrt[]{3} \\ \therefore A=27\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nvoop6g6mobp9lr0xqegbx66yq5uzuaz0p.png)
Hence, the area of the triangle is,
![27\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/9utvetk4g4d9kvbns4bbnwu54e52ws5sia.png)
Final answers
![\begin{gathered} \text{Perimeter}=18\sqrt[]{3} \\ \text{Area}=27\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/byuuwq8r6d42ozus7yenzgewzihacrx3q8.png)